Introduction
I adapted this game from one in the math circle book (p86) called "More likely, less likely". It's a very simple game which introduces the idea of probability and involves simple arithmetic.
Playing the game
For this game, you will need:
- Pen, paper and ruler to make the board
- Some tokens (coins, small toys, or bits of paper)
- Two six-sided dice
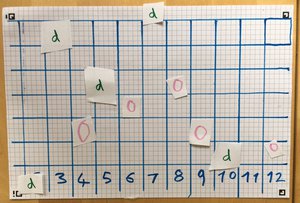
To make the board, draw an 11 by 7 grid (the height is not important, but 7 fit nicely on my paper). Number the squares along the bottom row 2 - 12.
The rules:
- Players take turns to put a counter on a number without a counter already on it.
- Keep going until everyone has placed five counters (or fewer if more than two players are playing).
- Players take turn to roll the two dice and add the two values.
- The player whose counter is in that column (if there is one) moves their counter one space forward.
- The winner is the first player to have a counter (or all their counters) reach the final row.
Our experience
The first time I played this with my five year old we picked two numbers each, using counters from another game. He chose 7 and 10, and his counter on 7 won.
For the second game (pictured), we made our own counters because with two counters each there's a good chance that no one gets to move. He really enjoyed cutting out the counters, possibly more than he enjoyed the game itself.
In this game, I picked 7, which again won (I also did surprisingly well with a counter on 3). When we played a third time, I think the counter on 10 won.
I was surprised how much my son enjoyed this game given how simple it is. In terms of education, he was very motivated to add the numbers on the dice. He tended to count the dots, so I started covering the dice and telling him to two numbers instead, especially for simpler sums. I imagine playing the game a lot would help improve small number addition.
It was pleasing that the counter on 7 won twice, which is the most likely result, but far from certain. I asked why he thought 7 would win more often while the counter at 2 barely moved, but I didn't get very far (and we ran out of time).
Later, I got him to fill out a table like this one. It was good arithmetic practise, and he quickly noticed the patterns so could fill it in easily. I tried asking some questions about which sums were most common, but he wasn't very interested, so I didn't push it.
Additional notes
In the original game, the numbers went from 1 - 15, so some of the numbers were impossible to get. I wish I had at least included 1, it's just the squared paper I was using divided nicely into 11 squares.
The original game also had players place one big counter and two smaller ones, giving more points for getting the big counter to the end. I think the purpose of this is to get players to assign a value to each number, but I thought it would overly complicate the game.
About nine months after we first played this game, I found this article about the game, by Marilyn Burns who called it "One of My All Time Favorite Games". She wrote about different ways to explore the game with children of different ages. Before she played the game, she asked her class to think about the possible ways to make the numbers 2 to 12.
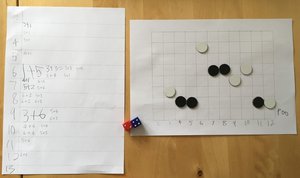
So, we played the game again, this time making a note of all the sums we got. I think it worked quite well for showing why the central numbers were more likely to win than the numbers at the extremes. At one point he noticed that 1 + 2 is the only way to make 3. I think playing the game a few more times, doing this, should make it more obvious what's happening.